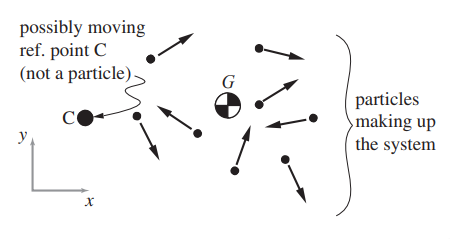
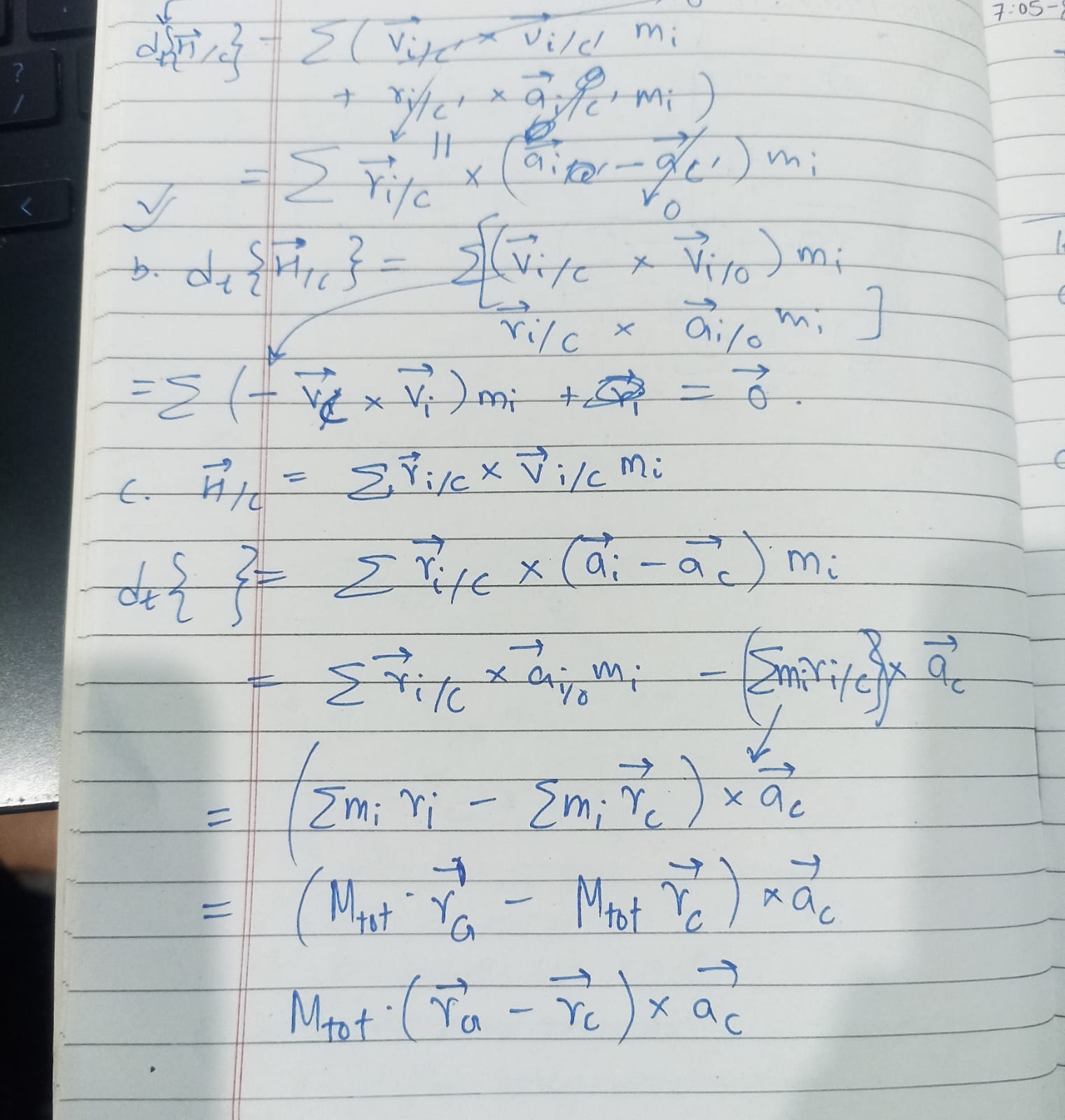problem19
1 \(\vec{H}_{/C} = \sum \vec{r}_{i/C'} \times \vec{v}_{i/C'} m_i\), where C’ is a point fixed in \(\mathcal{F}\) that instantaneously coincides with C. (Hint: this definition is good one, always!)
No conditions, this definition of \(\vec{H}_{/C}\) is consistent with \(\vec{F} = m\vec{a}\).
2 \(\vec{H}_{/C} = \sum \vec{r}_{i/C} \times \vec{v}_{i/0} m_i\). (This strange definition is used in the classic, but in this case odd, Dynamics book by Housner and Hudson.)
This definition of \(\vec{H}_{/C}\) is not consistent with \(\vec{F} = m\vec{a}\), unless \(\sum \vec{v}_C \times \vec{v}_{i/0} m_i = \vec{0}\), i.e C is moving perpendicular to every point in the rigid body. If C=G, then this definition becomes consistent, as no relative radial velocity.
3 \(\vec{H}_{/C} = \sum \vec{r}_{i/C} \times \vec{v}_{i/C} m_i\). (Hint: this is the most important candidate definition, but it’s only good for special kinds of C, namely: C = COM, C is fixed and …?)
This definition of \(\vec{H}_{/C}\) is not consistent with \(\vec{F} = m\vec{a}\), unless \((\vec{r}_G - \vec{r}_C) \times \vec{a}_{i/0} M_tot = \vec{0}\), i.e C is moving accelerating perpendicular to direction connecting C and G. If C=G, then this definition becomes consistent.