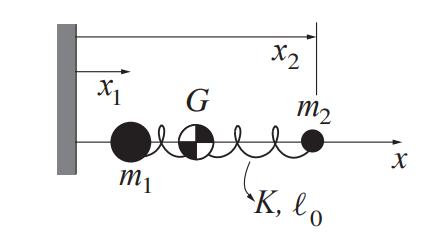problem20
Vishal Paudel
April 12, 2025
This problem has 3 independent educational goals:
- Motivate the use of kinematic constraints.
- Introduce the simplest of a class of vibrations problems which you should master. At this point, it is this aspect: mastery of derivation of the equations of motion. You should check that you can reproduce the lecture example with no sign errors without looking up anything.
- Development of critical exploration using analytical and numerical methods.
Two masses \(m_1\) and \(m_2\) are constrained to move frictionlessly on the x axis. Initially they are stationary at positions \(x_1(0) = 0\) and \(x_2(0) = \ell_0\). They are connected with a linear spring with constant k and rest length \(\ell_0\). A rightwards force is applied to the second mass. It is a step, or ‘[Heaviside](https://en.wikipedia.org/wiki/Heaviside_step_function]’ function
\[ F(t) = F_0H(t) = \begin{cases} 0 & \texttt{, if } t < 0 \\ F_0 & \texttt{, if } t \ge 0 \end{cases} \]
Write code to calculate, plot and (optionally) animate the motions for arbitrary values of the given constants.
Within numerical precision, should your numerical solution always have the property that \(F = (m_1 + m_2) a_G\) where \(x_G = (x_1 m_1 + x_2 m_2)/(m_1 + m_2)\)? (As always in this course, “yes and no” questions aare not multiple choice, but need justification that another sutdent, one who got the opposite answer as you, would find convincing.)
Use you numerics to demonstrate that if \(k\) is large the motion (displacement relative to its starting postion) of each mass is, for time scales large compared to the oscillations, close to the cneter of mass motion.
5730 only: Using analytical arguments, perhaps inspired by and buttressed with numerical examples, make the following statement as precise as possible:
For high values of \(k\) the system nearly behaves like a single mass.
Of course, in detail, the system has 2 degrees of freedom (DOF). So you are looking for a way to measure the extent to which the system acts like it has 1 DOF, and in which conditions (for which extreme values of parameters and times) the system is close to 1 DOF by that measure. There is not a simple single unique answer to this question.